
Добиться бесшовной графики на раппортах можно тремя подходами. По примеру плиток Труше, восточных орнаментов Гирих и Маурица Эшера.
1. Плитки Труше известны в нескольких вариациях. С растиражированным узором из двух треугольников контрастных цветов, так сильно полюбившиеся испанцами. И квадратов с рисунком обладающим вращательной симметрией второго порядка, т.е. совпадающие сами с собой дважды при повороте на 180°.


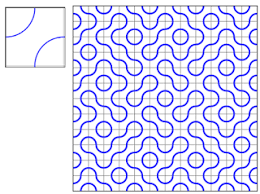
Один из упомянутых релизов - набор паттернов Mosaic flowers - построен по примеру плиток Труше. Квадраты дополнены треугольниками и вытянутым шестиугольником.

2. Гирих – это набор из пяти плиток-раппортов, использовавшихся для создания геометрических орнаментов исламской архитектуры примерно с двенадцатого века. Примечательную историю переоткрытия гирихов опустим. Достаточно упомянуть наличие их связи с мозаикой Пенроуза и треугольниками Робинсона.
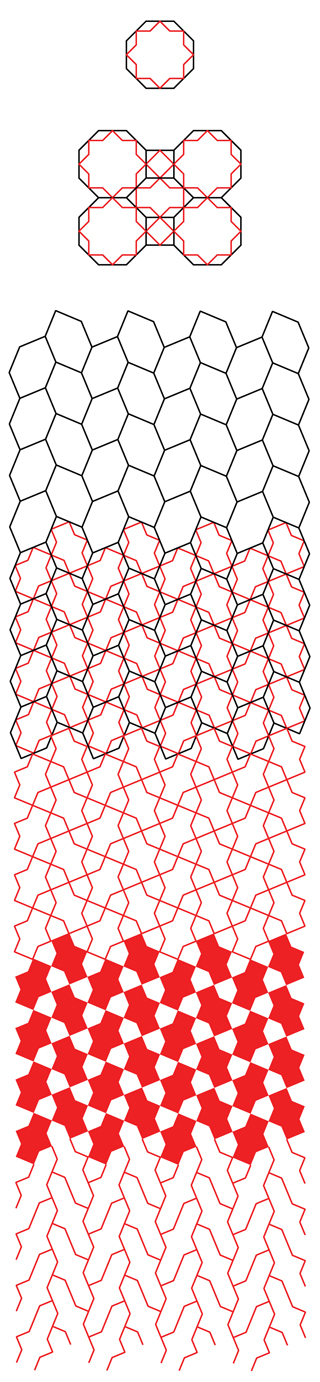
2.1 Опираясь на иллюстрацию в виде косы, рассмотрим как наносить бесшовную графику на гирихи. Пользуясь приемами описанными ранее и ключом с иллюстрации ниже, строим базовые плитки. В данный момент получились: восьмиугольник, квадрат и шестиугольник. Все они являются параллелогонами, т.е. их стороны равны и попарно параллельны.
2.2 Из срединной точки стороны параллелогона строим лучи с внутренним углом 45°, так чтобы его биссектриса совпала с нормалью к стороне многоугольника. Затем удаляем их взаимные пересечения добиваясь вида как на иллюстрации.
2.3 Комбинацией из полученных фигур выкладываем бесконечную мозаику, а затем прячем стороны плиток.
3. Орнаменты Эшера требуют особого рассмотрения по причине использования цветной симметрии. Рекомендую статью Ольги Чигинцевой “Цветная симметрия в сетчатых орнаментах с преобразованиями подобия”.
Примечание. Осторожней с мозаикой Пенроуза в сочетании с цветной симметрией. Ученый оформил тучу патентов и уже судился с производителем туалетной бумаги.
#орнамент #паттерн #многораппортный #плитки_труше #гирих #mosaic_flowers


